数字图像取证 - 基于相机属性的取证 1

Posted on Fri 03 July 2020 in Digital Image Forensics • 1 min read

CFA

在数字图像中，CFA是位于图像传感器之前的一组用于过滤色彩，收集色彩信息的镜片。由于数码相机传感器仅测量光线的明亮程度无法对色彩做出处理，通过CFA为每一个像素赋予其色彩。下图是Bayer Array CFA也是最常见的CFA, 使用该CFA导致了实际只有1/3的色彩信息能被cmos保存下来，另外的2/3只能利用插值算法进行填充得来的。那么不同的相机之间由于不同的cmos以及插值算法就会有不同的特征存在。

对于一张Raw图像其每个像素点的RGB构造方式为

$$ \begin{aligned} \tilde{R}(x, y) &= S(x, y) &if S(x, y) = r_{x, y} \\ &= 0 &otherwise\\ \tilde{G}(x, y) &= S(x, y) &if S(x, y) = g_{x, y} \\ &= 0 &otherwise\\ \tilde{B}(x, y) &= S(x, y) &if S(x, y) = b_{x, y} \\ &= 0 &otherwise\\ \end{aligned} $$

再结合插值算法，一个RAW图像RGB像素则抽象为

$$ \begin{aligned} R(x, y) = \sum^N_{u, v = -N}h_r(u, v)\tilde{R}(x - u, y -v) \\ G(x, y) = \sum^N_{u, v = -N}h_r(u, v)\tilde{G}(x - u, y -v) \\ B(x, y) = \sum^N_{u, v = -N}h_r(u, v)\tilde{B}(x - u, y -v) \\ \end{aligned} $$

其中$h()$为不同的插值滤波器，如$h = (\frac{1}{2}, 1, \frac{1}{2})$ 就是一个双线性插值算法，对其做一个外积就变成了2维的双线性插值算法。

当然插值算法不仅仅是双线性一种，不同的相机厂商都有不同的插值算法比如基于中位数的，基于梯度的或者基于自适应色彩平面的等等。就是这些不同的滤波方法就导致了不同的色彩下有了特点的统计信息。下面我们假设存在这样一种插值算法

$$ \begin{aligned} R(2x + 1, 2y) &= \frac{R(2x + 1, 2y - 1)}{2} + \frac{R(2x + 1, 2y + 1)}{2}\\ R(2x, 2y + 1) &= \frac{R(2x - 1, 2y + 1)}{2} + \frac{R(2x + 1, 2y + 1)}{2}\\ R(2x, 2y) &= \frac{R(2x - 1, 2y - 1)}{4} + \frac{R(2x - 1, 2y + 1)}{4} \\ &+ \frac{R(2x + 1, 2y - 1)}{4} + \frac{R(2x + 1, 2y + 1)}{4} \end{aligned} $$

也就是说每一个像素都完美的于其周围的像素相关，反而言之某些非插值的图像中的像素不会于其周围的像素相关。进一步的，如果图像被修改，那么由于不同的插值算法的影响，像素的相关性就会被破坏。但是，由于我们并不知道像素于像素之间是否真的相关或像素于像素之间的相关关系（插值方法）所以我们无法直接的利用上方的方法，但是EM算法可以解决我们什么都不知道的问题。我们假设f（x）是一组型号，他来自于两组模型，线性插值的m1模型也就是他与其邻居线性相关$f(x) = \sum^N_{u = -n}\alpha_u f(x + u)$以及与其邻居不相关的m2模型.

基于EM算法检测CFA插值情况

下面利用EM算法对两组模型进行验证: 在E-step, 利用残差求解似然$\omega$

$$ \begin{aligned} r_1(x) = f(x) -\sum^N_{u = -N}\alpha_uf(x + u)\\ w_1(x) = P_r(\alpha | r_1(x)) = \frac{\frac{e^-r^2_1(x)}{\sigma}}{\frac{e^-r^2_1(x)}{\sigma} + \frac{1}{\delta}} \end{aligned} $$

在M-Step, 利用先前求解出的似然$\omega$, 来估计参数$\alpha$. 首先我们利用SE求误差

$$ E(\alpha) = \sum_\alpha \omega_1(x)(f(x)- \sum^N_{u = -N}\alpha_u f(x + u))^2 $$

随后对误差求梯度并设置梯度为0, 得到

$$ \alpha = (F^TWF)^{-1}F^TWf $$

对于图像而言, 即二维数据的情形我们首先假设

$$ f(x) = \sum^N_{u, v = -n}\alpha_{u, v} f(x + u, y + v) $$

随后求解似然

$$ \omega_1(x, y) = P_r(\alpha | r_1(x, y)) = \frac{frac{e^{r^2_1(x, y)}{\sigma}}}{frac{e^{r^2_1(x, y)}{\sigma}} + frac{1}{\sigma}} $$

计算误差

$$ E(\alpha) = \sum_{x, y}\omega_1(x, y)(f(x, y) - \sum^N_{u, v = -N}\alpha_{u, v}f(x + u, y + v))^2 $$

最后求解$\alpha$

$$ \begin{aligned} \sum^N_{u, v =-N}\alpha_{u, v}(\sum_{x, y}\omega_1(x, y)f(x + s, y + t)f(x + u, y + v)) = \\ \sum_{x, y}\omega_1(x, y)f(x + s, y + t)f(x, y) \\ \end{aligned} $$

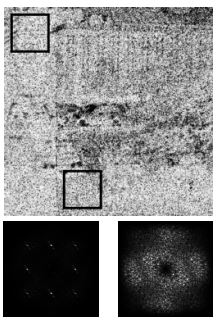
利用求解出的a，那么就可以刻画相邻的像素之间的相关概率，见下图，其中左侧是原图，中间是相关概率图，右侧是利用傅里叶变化处理后的概率图 cfa_em 通常经过特定插值算法的图像的傅里叶变换图,都会有明显的傅里叶峰, 在图像中表现为明显的小点.